Inflation and the Cosmic Microwave Background
Inflation is a model proposed to explain numerous "coincidences" in our universe: lack of monopoles or relic particles, spatial flatness, thermal isotropy of the CMB, etc. Inflation's superluminal expansion of 60 e-foldings dilutes away relic particles, flattens space, and thermalizes the observable universe. It also amplifies quantum fluctuations in the gravitational metric to cosmic scales, pushing them outside the causal horizon only to re-enter much later. Scalar perturbations, or gravitational wells, seed large scale structure and they generate the temperature anisotropies in the Cosmic Microwave Background (CMB), light released when atoms first formed. Some of the modes are super-horizon in scale when the CMB is released, and smaller causally connected ones drove acoustic oscillations, all initially synchronized by inflation. The resulting harmonic structure in the CMB temperature anisotropies, as well as flatness inferred from the spectral peak locations, strongly support inflation.
Cosmic Gravitational Wave Background

Gravitational Lensing
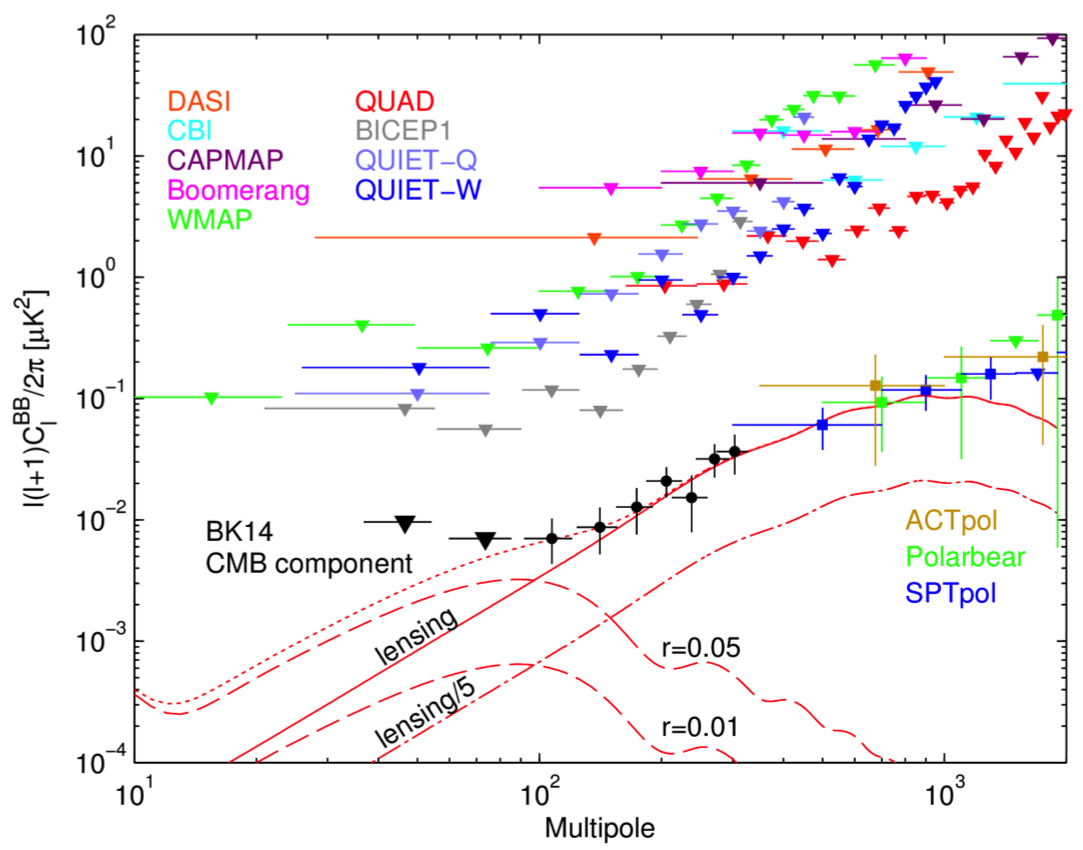
CMB photons experience gravitational lensing by large scale structure, deflecting photon trajectories and moving around the temperature features in the CMB. This converts even symmetry E-mode polarization into a mixture of E and B, forming a non-primordial foreground with the same spectrum as the original CMB. BICEP-2 and Keck are also sensitive to lensing B-modes (5.5 σ detection from BB autospectrum), seen on the right side of the spectrum above.
Below is an animated illustration from the Planck team of CMB lensing:
If r>0.02, the tensor spectrum may dominate the lensing one at degree scales, but is obscured by lensing at finer scales less than one degree; if r is less than this, then lensing will dominate at all scales. Exploiting non-gaussian features in the lensing spectrum that correlate different angular scales, we can in principle partially remove lensing. The instruments with the greatest sensitivity to this effect will have large apertures that can resolve arcminute deflections. In particular, our neighbors, South Pole Telescope, can map our field and assist in de-lensing our maps. Despite our limited 30' resolution, our deep maps with BICEP/Keck do let us constrain the lensing potential, as shown below. This spectrum of the lensing potential is the highest significance detection of lensing to date through EB polarization correlations (5.8 σ through EB estimators) shows the degree scale correlations and also matches the lensing potential amplitude measured by Planck and other experiments. (ALφφ=1.15 ± 0.36)
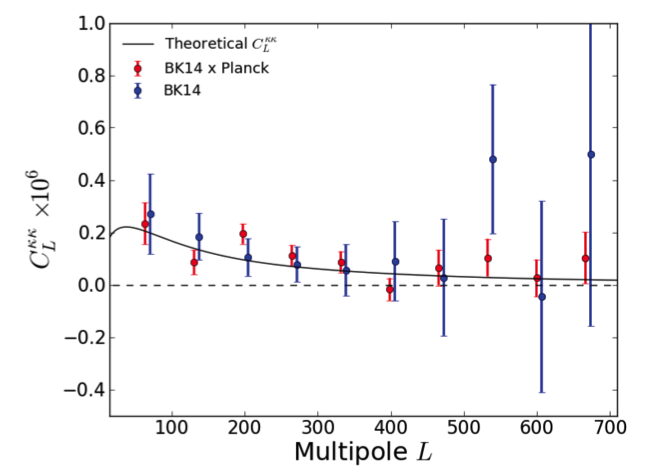
The lensing spectrum itself is sensitive to the sum of neutrino masses of different generations—- massive neutrinos suppress structure formation and thus lensing at small scales. Such measurements may resolve the neutrino hierarchy problem and allow us to test seesaw mechanisms.

Extensions to the Standard Model of Particle Physics
CMB polarization can also be used to test some extensions of the Standard Model of Particle Physics. Nearly massless Nambu-Goldstone bosons could couple to photons through a Chern-Simon’s extension to the lagrangian of the form
where Fμν is the electromagnetic tensor, φ and M are the new pseudo-scalar field and associated mass, and β is a coupling term between photons and the new field. The additional non-maxwell terms are not ruled out by existing experimental data and string theory generically predicts that such fields should exist. However, if they do exist, they would break CPT symmetry- an important cornerstone of quantum field theory and 20th century particle physics.
This coupling would also modify Maxwell’s Equations to produce different dispersions for left and right circularly polarized photons. So photons that propagate over cosmological distances experience a birefringence that rotates the linear polarization by α due to a change in the field Δφ during travel from last scattering.
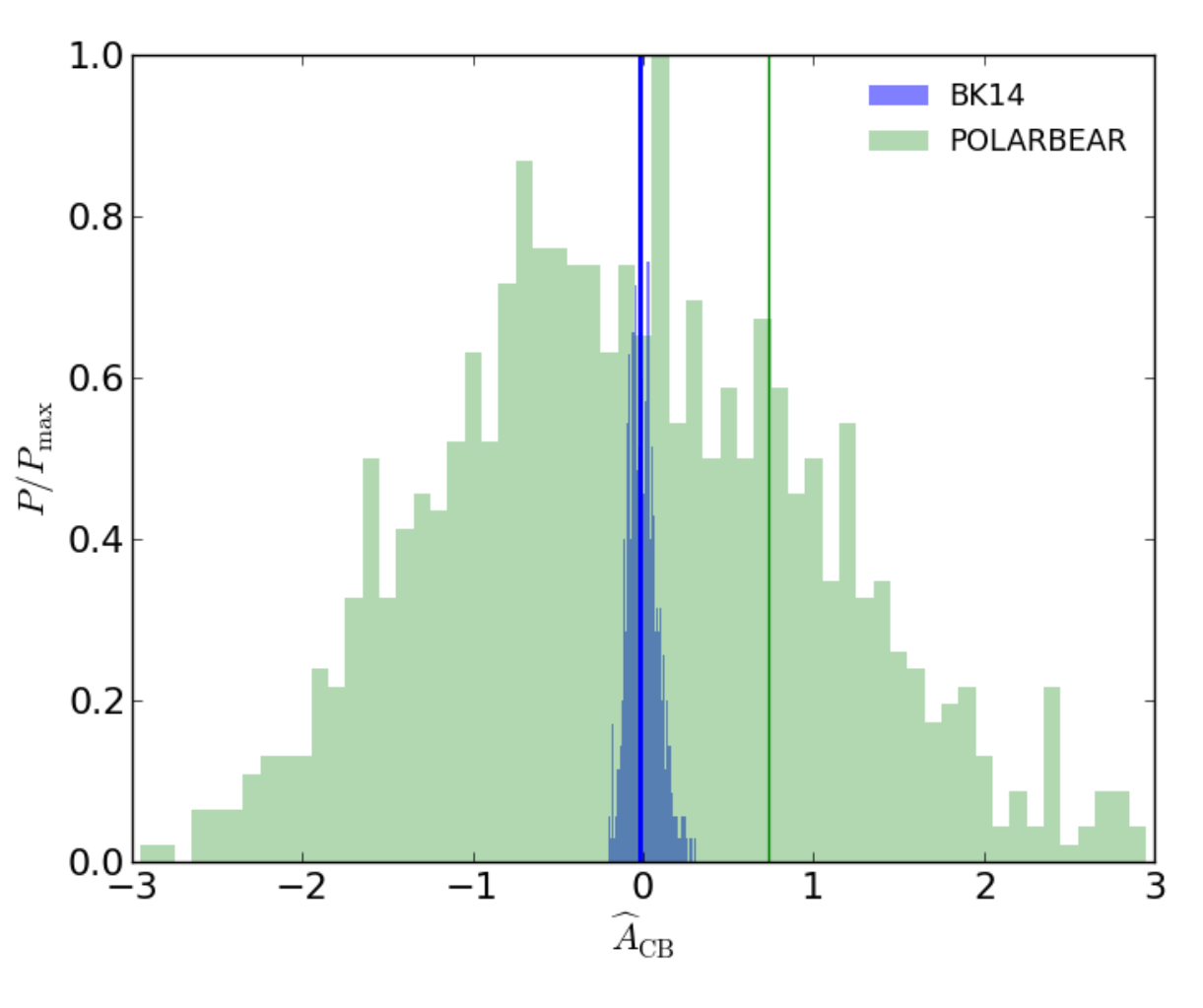
Such rotations would correlate the E and B spectra at large scales in a way that is spectrally invariant. Our team and others are searching for such effects in our data, but have not found evidence of them to date. Currently, we are systematically limited by our ability to calibrate the polarization angles of the detectors in our instruments. However, some models predict anisotropic birefringence, and we have used our data to place tight limits on such effects, as seen in the histogram below:
Epoch of Reionization
The optical depth to reionization has an important degeneracy with r in tradiational TT measurements fo the CMB. In fact, the epoch of reionization, when the stars began to burn, is poorly understood in its own right and calls out for deeper understanding. Numbers on the end, mid-point, and duration of reionization respectively from quasar spectra, CMB polarization, and kinetic Sunyaev-Zeldovich effects are in slight tension.
The following simulation from Gnedin, et al. illustrates one possible way that reionization may have unfolded. Blue is neutral hydrogen.Cosmologists suspect that the IGM reionized from UV photons produced in early quasars or protostars. 21-cm tomographic line mapping experiments attempt to follow this process using neutral hydrogen as a tracer. In the Tomographic Ionized carbon Mapping Experiment (TIME), we will use ionized carbon (CII) as a complimentary probe, forming power spectra for different redshifts. When emitted in the 5 < z < 10 range, CII's 160 μm wavelength redshifts into the 200-300GHz atmospheric window where we have several generations of expertise through CMB experiments. According to hierarchal models of reionization, Ionized Carbon (CII) emission from the epoch of reionization should anti-correlate with 21-cm HI emissions on large scales, but on small scales inside a bubble, the correlation must vanish. The length scale where this transition occurs should measured the ionized "bubble size," and measuring this as a function of redshift would reveal reionization's detailed history, experimentally producing the above simulation video. We hope to use such cross-correlations to test hypotheses about the underlying mechanisms of reionization. Caltech is moving the CSO to Chile and will likely install this instrument there in the future.
